Editing of 3D colored meshes

Nvidia Academic Hardware Grant scheme Principal Investigator: Olivier Lézoray, Professor Project participant: Zeina Abu-Aisheh, Post-Doctorate Normandie Université, UNICAEN, ENSICAEN, GREYC UMR CNRS 6072, Caen, FRANCE

Project Description

In the last two decades, we have witnessed enormous growth in digital data production and we have now entered the era of the so-called "Big Data". As a consequence, there is an explosion of interest in processing and analyzing very large datasets containing millions of entities. These datasets can be collected in very different settings and although apparently different from one another, all these datasets often require similar processing and analysis techniques: restoration, missing value completion, clustering, learning and inference, to quote but a few. With similar processing objectives that can operate on heterogeneous types of data, it is natural to seek a common representation of digital data that can ease the unification of information processing. Fortunately, graphs are a convenient data model for representing massive digital data sets in many applications. With such a unified representation, many information-processing tasks become graph analysis problems.

However, graphs are not only of interest for representing the data to facilitate its analysis, but also for defining graph-theoretical algorithms that enable the processing of data associated with both graph edges and vertices. Indeed, more generally, massive datasets represented as graphs can be seen as a set of data samples, with one sample at each vertex in the graph. In such a scenario, the high-dimensional data associated to vertices can be viewed as graph signals. Processing graph signals is different from usual graph analytics since a vector of data is associated with each vertex in addition to considering the relationships encoded by the graph edges: graph analytics only study the underlying relational structure of the graph data, such as communities or repeating patterns. Actually, there is emerging interest in the development of algorithms that enable the processing of graph signals: one might be interested in filtering, clustering, or compressing this structured type of signals.

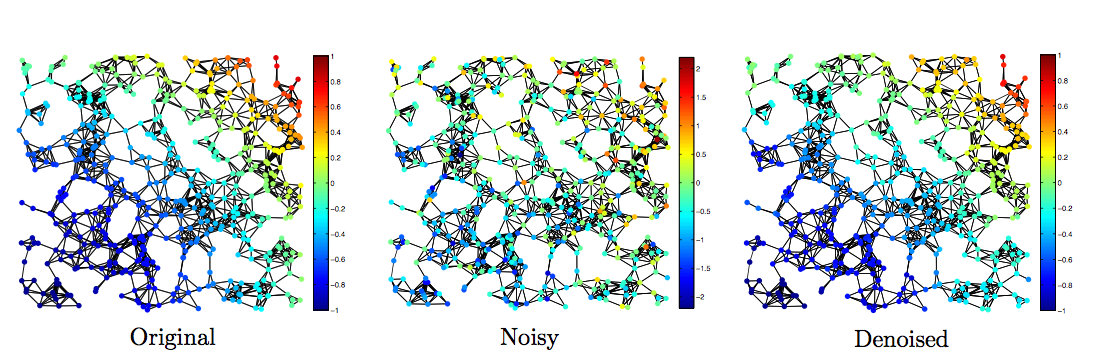
The analysis of graph signals faces several open challenges, mainly because of the combinatorial nature of the involved signals, which are not necessarily embedded in Euclidean spaces. This makes the use of classical signal processing methods difficult. As a result, the development of efficient methods that are able to deal with arbitrary graph signals is of paramount importance. The project falls within this line of research and proposes to develop an efficient methodology for the processing of specific graph signals: 3D colored meshes.

Recently, low cost sensors have brought 3D scanning into the hands of consumers. As a consequence, a new market has emerged that proposes cheap software that, similarly to an ordinary video camera, enables to generate 3D models by simply moving around an object or a person. With such software one can now easily produce 3D colored meshes with each vertex described by its position and color. However, the quality of the mesh is not always visually good and a typical user is often interested in enhancing the latter (for instance before to print it in 3D or to use it as an avatar in video games).

There is now a huge need for fast algorithms that enable to efficiently process large 3D colored meshes. Represented as graphs, a 3D colored mesh can be viewed as a signal (with both spatial and spectral information) living on an irregular graph. Most inverse problems that one can encounter in computer vision found their analogue for 3D colored meshes (denoising, completion, sharpening, segmentation, etc.). Ideally, a typical user would like to be able to perform all these tasks within some software, as everybody can do now in softwares such as Photoshop for images. However, 3D colored meshes are massive datasets that do contain millions of vertices and their processing is very computationally demanding.

We have recently developed graph signal processing algorithms for the manipulation of 3D colored meshes. For instance, we have proposed a method for the automatic sharpness enhancement of 3D colored meshes. Existing techniques for sharpness enhancement of images use structure-preserving smoothing filters within a hierarchical framework. They decompose the image into different layers from coarse to fine details, making it easier for subsequent detail enhancement. Some filters have been extended to 3D meshes but most manipulate only mesh vertices positions. In our approach we have developed a robust sharpness enhancement technique based on morphological graph signal decomposition. The approach considers manifold-based morphological operators to construct a complete lattice of vectors. With this approach, a multi-layer decomposition of the 3D colored mesh, modeled as a graph signal, is proposed that progressively decomposes an input color mesh from coarse to fine scales. The layers are manipulated by non-linear s-curves and blended by a structure mask to produce an enhanced 3D color mesh.

Original Colored Mesh from Reconstruct Me	Structure Mask	Sharpened Colored Mesh

Original/Sharpened Colored Mesh (roll over/out the image to see the difference)

However, if structure preserving smoothing filters have became so popular in image processing, this is mainly because they have been made very fast with the use of graphics cards. For 3D colored meshes, the current offline methods we have developed can take several minutes to get results on a modern CPU. Such a long processing time is not acceptable for interactive processing with a user. Since we consider graph signals, most of the processing time is highly parallelizable. In this project we plan to utilize the massive parallel processing power of the GPU to accelerate our processing of 3D colored meshes.

Acknowledgments

We gratefully acknowledge the support of NVIDIA Corporation with the donation of the Titan Xp GPU used for this research.